logistic regression
Stephen Skalicky
2024-12-18
Getting logistical
library(tidyverse)
library(palmerpenguins)
library(emmeans)
data(penguins)
penguins <- drop_na(penguins)What better way to ring in the new year than by looking at a completely different \(y\) variable related to penguins? That’s right, today we are going to take a closer look at the left side of the regression equation to talk about what happens when our outcome variable is not a number.
Specifically, we are going to look at how to model our outcome variable when it is a binary outcome: yes/no, true/false, correct/incorrect, or, in the case of our penguins, male/female.
This type of regression is called a logistic regression.
Here is the formula:
\[ \Large\text{logit}(P(Y=1)) = \ln\left(\frac{P(Y=1)}{1 - P(Y=1)}\right) = \beta_0 + \beta_1 X_1 + \beta_2 X_2 + \ldots + \beta_k X_k \]
Yikes…while the right-hand side of the formula looks the same as the other regression syntax, the left-hand side is quite different. But we can understand this by thinking about something we probably already know about: the odds of something happening.
- \(P\) is the probability of something
- so \(P\)(\(Y\) = 1) means the probability of our outcome variable being 1 (versus 0)
- Dividing the probability of something being 1 over the inverse gives us the odds of the outcome.
\[ \Large\frac{P(Y=1)}{1 - P(Y=1)} \]
For example, assume you had a population of penguins where 80% were male and 20% were female. Let’s code female as 0 and male as 1.
\[ \large\frac{P(Y=\text{male})}{1 - P(Y=\text{male})} \]
The probability of being a male penguin would be 80% or .8. The odds would then be:
\[ \large\frac{0.8}{1-0.8} \]
Which gives us the answer of \(4\) - there is \(4:1\) odds that any one penguin will be male compared to female, or four times more likely.
## [1] 4What if exactly half of the penguins were male and half were female? The odds would be \(1:1\) - equal chance:
## [1] 1And if only .1% were male? Almost \(0:1\) odds…
## [1] 0.01010101what happens with odds in a linear regression?
So what would happen if we fit this as a continuous variable? We would have a \(Y\) variable that goes from \(0\) to \(\infty\). The predictions would be trying to show how a one-unit increase in an \(X\) are associated with some sort of increase in the odds. This is not really a continuous variable like body mass or flipper length.
the \(ln\) function
We need a way to convert the odds into a more reasonable measure so that we can apply the regression formula. This is what the \(ln\) around the odds is - it stands for the natural logarithm. Without going into too much detail, we can think about the natural logarithm as the inversion of exponential growth in a number.
Because odds can grow to infinity, we need to bound that number into a more realistic number line. The nice thing about logged odds is that we can easily convert between the inverted logarithm and exponentiation.
## [1] 1.386294## [1] 4Look at what happens to this range of very different values when we apply the natural logarithm:
some_numbers = c(0.00001,1,5,10,4000,9e10)
for(number in some_numbers){
print(str_glue('Original value: {number} \t Natural logarithm of value: {round(log(number),3)}'))
}## Original value: 1e-05 Natural logarithm of value: -11.513
## Original value: 1 Natural logarithm of value: 0
## Original value: 5 Natural logarithm of value: 1.609
## Original value: 10 Natural logarithm of value: 2.303
## Original value: 4000 Natural logarithm of value: 8.294
## Original value: 9e+10 Natural logarithm of value: 25.223natural log of odds ratio = the logit
So, now we know that the logit of the probability of a
\(Y\) being 1 is the natural logarithm
of the odds ratio - our dependent variable in the regression is
transformed into a logit in order to describe the effects of \(x\) on \(y\).
\[ \large\text{logit}(P(Y=1)) = \ln\left(\frac{P(Y=1)}{1 - P(Y=1)}\right) \]
how to do a logistic regression
A logistic regression is very similar to a continuous, we just need
to use glm instead of lm. The glm
stands for generalised linear model, a confusing term
indeed, but basically lets us fit different families of distributions
and different “link” functions which tells the regression how to “deal”
with the distribution of the dependent variable.
For a logistic regression, we use family = binomial to
tell the model that our outcome is a categorical binary variable. We
then use link = logit to tell the model we want to
transform the outcome variable into logits - a logistic
regression.
Otherwise, the syntax is the same as lm.
glm(dv ~ x1 + x2.., family = binomial(link = 'logit'), data = dat)inspect distribution of penguins
We can see that the data has a relatively balanced set of penguins, with almost exactly 50:50 ratio of male to female in the data set. So we see that species is probably not a predictor of penguin sex.
# plot the gender distributions of penguins
penguin_plot <- penguins %>%
group_by(species, sex) %>%
summarise(count = n())## `summarise()` has grouped output by 'species'. You can override
## using the `.groups` argument.ggplot(penguin_plot, aes(y = count, x = species, fill = sex)) +
geom_col(position = 'dodge') +
scale_fill_brewer(palette = 'Set2')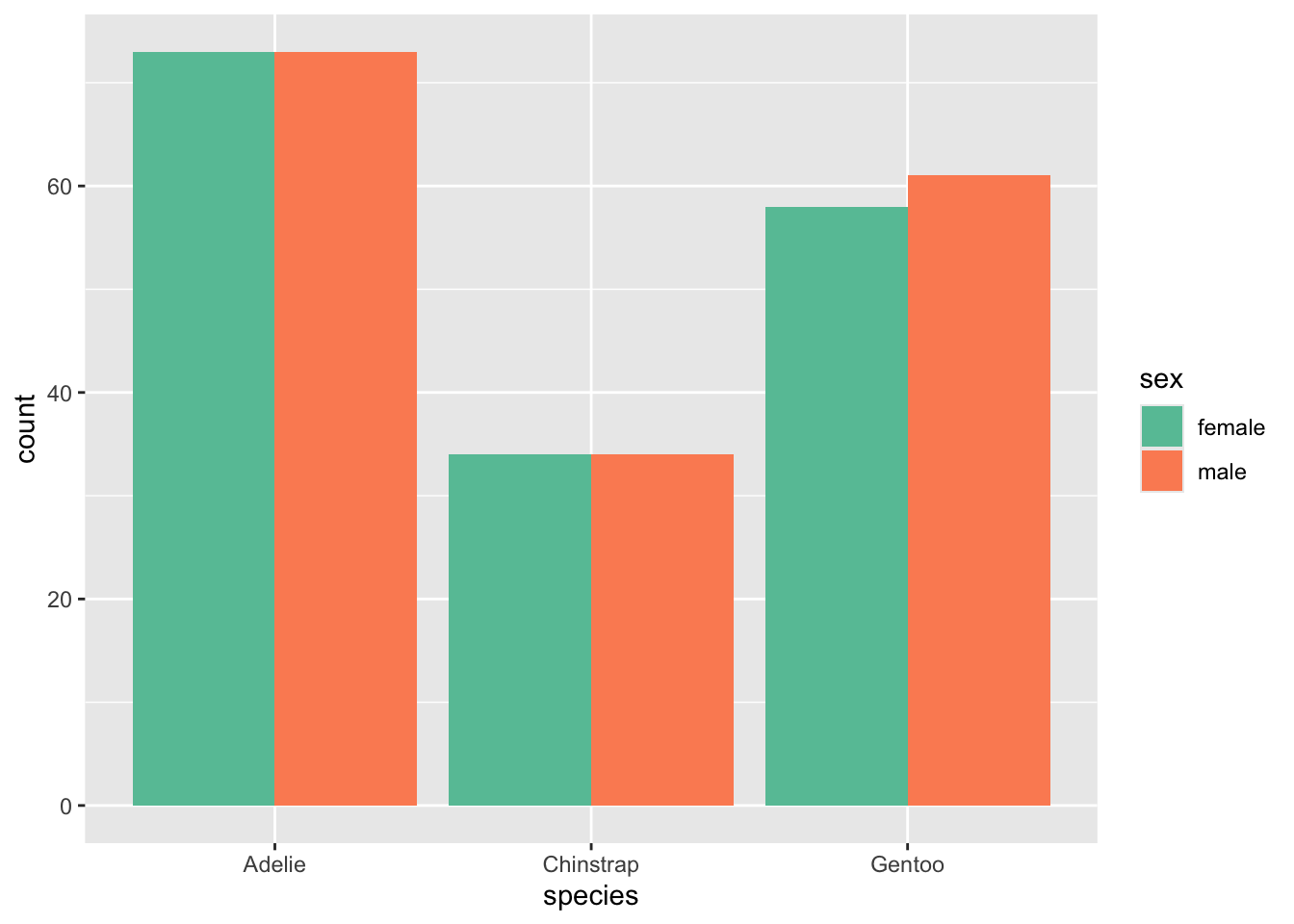
We also know that sex is not distributed equally across body mass!
plot(penguins$body_mass_g, col = penguins$sex)
legend('topright', legend = levels(penguins$sex), col = 1:2, pch = 1)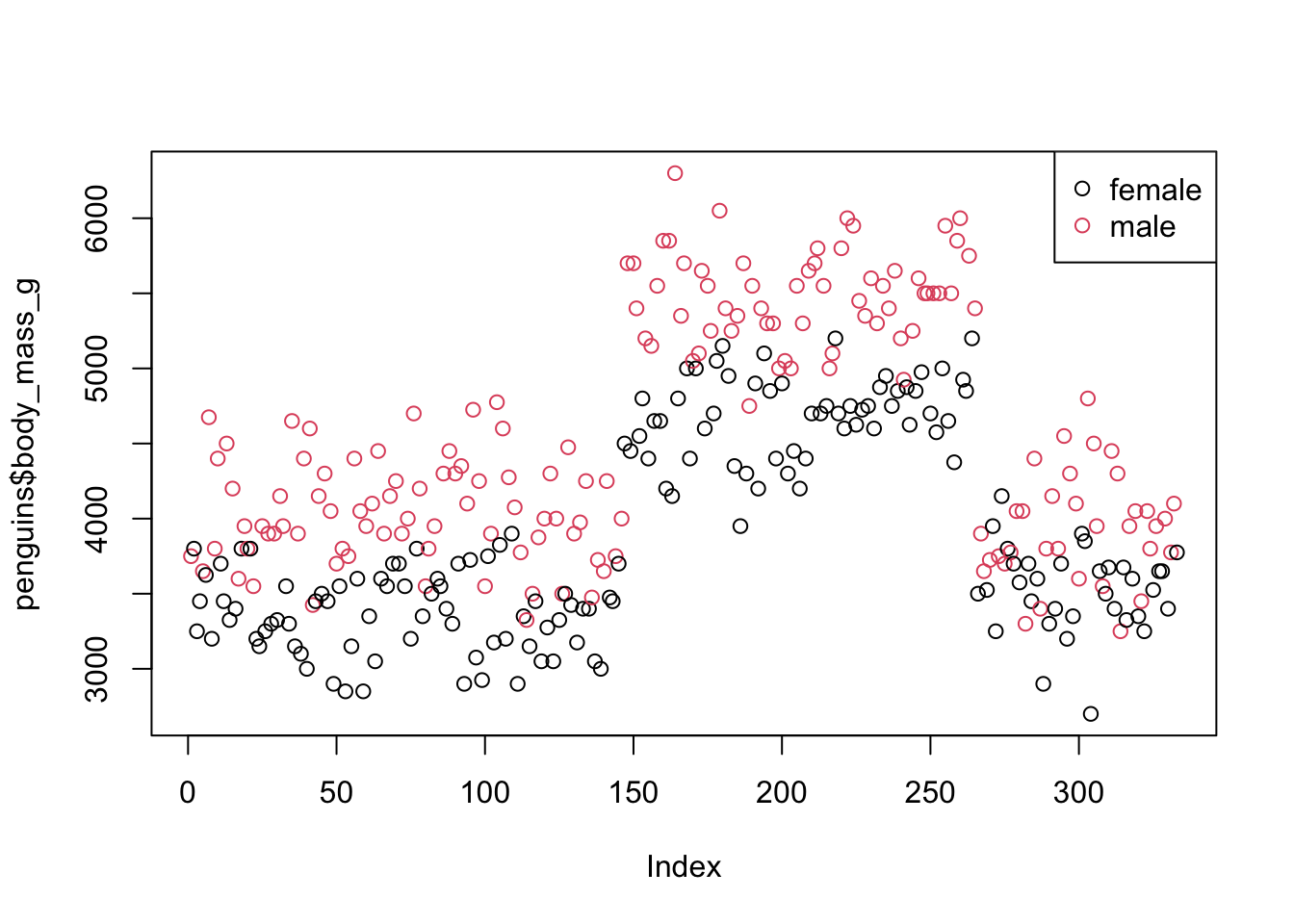
predict sex with body mass
We do know that body mass in penguins is strongly associated with being male or female, in that male penguins are bigger than female penguins. So lets flip the script and predict sex with body mass.
Here is the simple one predictor regression model:
# fit a logistic regression predicting sex from body mass:
m1 <- glm(sex ~ body_mass_g, family = binomial(link = 'logit'), data = penguins)
summary(m1)##
## Call:
## glm(formula = sex ~ body_mass_g, family = binomial(link = "logit"),
## data = penguins)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -5.1625416 0.7243906 -7.127 1.03e-12 ***
## body_mass_g 0.0012398 0.0001727 7.177 7.10e-13 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 461.61 on 332 degrees of freedom
## Residual deviance: 396.64 on 331 degrees of freedom
## AIC: 400.64
##
## Number of Fisher Scoring iterations: 4How do we interpret this? We do so in the same way as the
lm regressions. The intercept is the predicted logit value
of our outcome variable, and the estimates are the effects of the
predictor variable. However, now that our outcome variable is expressed
in terms of logits, it becomes far more difficult to make any sense of
these estimates.
But, this says that each one-unit increase in body mass is associated with an increase of .001 logits from the intercept. Females are the baseline, coded as 0, whereas males are coded as 1. So positive effects indicate a movement towards 1 (in this case, a movement towards male).
The interpretation is therefore that a one-unit increase in body_mass_g increases the probability of a penguin being male by 0.001 logits. This might seem small, but keep in mind this is on a logarithmic scale.
back transforming the logit
However, we can easily convert the logit back to an odds scale, because the logarithm can be inversed using exponentiation. The estimate for the effect of body mass increase was 0.0012398, so the odds ratio would be:
## [1] 1.001241We can think of odds ratio as a percentage. If an odds ratio of 1 = equal odds, then an odds ratio of 1.001241 is slightly above equal odds. Converting the ratio to a percentage means subtracting 1 from the value and then multiplying by 100:
## [1] 0.1241So a one-gram increase in body mass is associated with a 12% increase in the odds that a penguin will be male compared to female.
using emmeans
the emmeans package lets us swap between these as well.
Note the message given here - that the results are on the
logit scale, NOT the response scale. You should understand
what this means now - the response scale is the original scale, which is
expressed as frequency tallies or percentages. The logits were formed as
part of the model building process.
## body_mass_g emmean SE df asymp.LCL asymp.UCL
## 4207 0.0534 0.122 Inf -0.185 0.292
##
## Results are given on the logit (not the response) scale.
## Confidence level used: 0.95We can ask for the results to be expressed on the original scale, which is expressed a probability. How to interpret this output? When body_mass_g is held at the mean, 4207, there is a 51.3% chance that the penguin is a male penguin. That’s almost even odds (e.g., odds ratio of 1).
## body_mass_g prob SE df asymp.LCL asymp.UCL
## 4207 0.513 0.0304 Inf 0.454 0.573
##
## Confidence level used: 0.95
## Intervals are back-transformed from the logit scaleUsing emtrends, we get the statistical effect (or slope,
trend, whatever) of body mass on sex, which is the same 12% discussed
above:
## body_mass_g body_mass_g.trend SE df asymp.LCL asymp.UCL
## 4207 0.00124 0.000173 Inf 0.000901 0.00158
##
## Confidence level used: 0.95We can plot the probabilities at different emmeans to show the probability contours, which is an incredibly intuitive way to visualise the effects of a logistic regression.
Because the level female in the variable
sex was the baseline, coded as 0, the model is trying to
predict the probability of male, which was coded as 1.
Here, they y-axis is the percentage likelihood the outcome variable will
be 1 (i.e., sex == male).
prob_plot <- as.data.frame(emmeans(m1, ~body_mass_g, type = 'response', at = list(body_mass_g = seq(min(penguins$body_mass_g), max(penguins$body_mass_g), length.out = 100))))
ggplot(prob_plot,(aes(y = prob, x = body_mass_g))) +
geom_ribbon(aes(ymin = asymp.LCL, ymax = asymp.UCL), alpha = .25, fill = 'salmon') +
geom_line(lty = 'dashed') +
labs(title = "Increasing probabilty of sex = male as body mass increases.")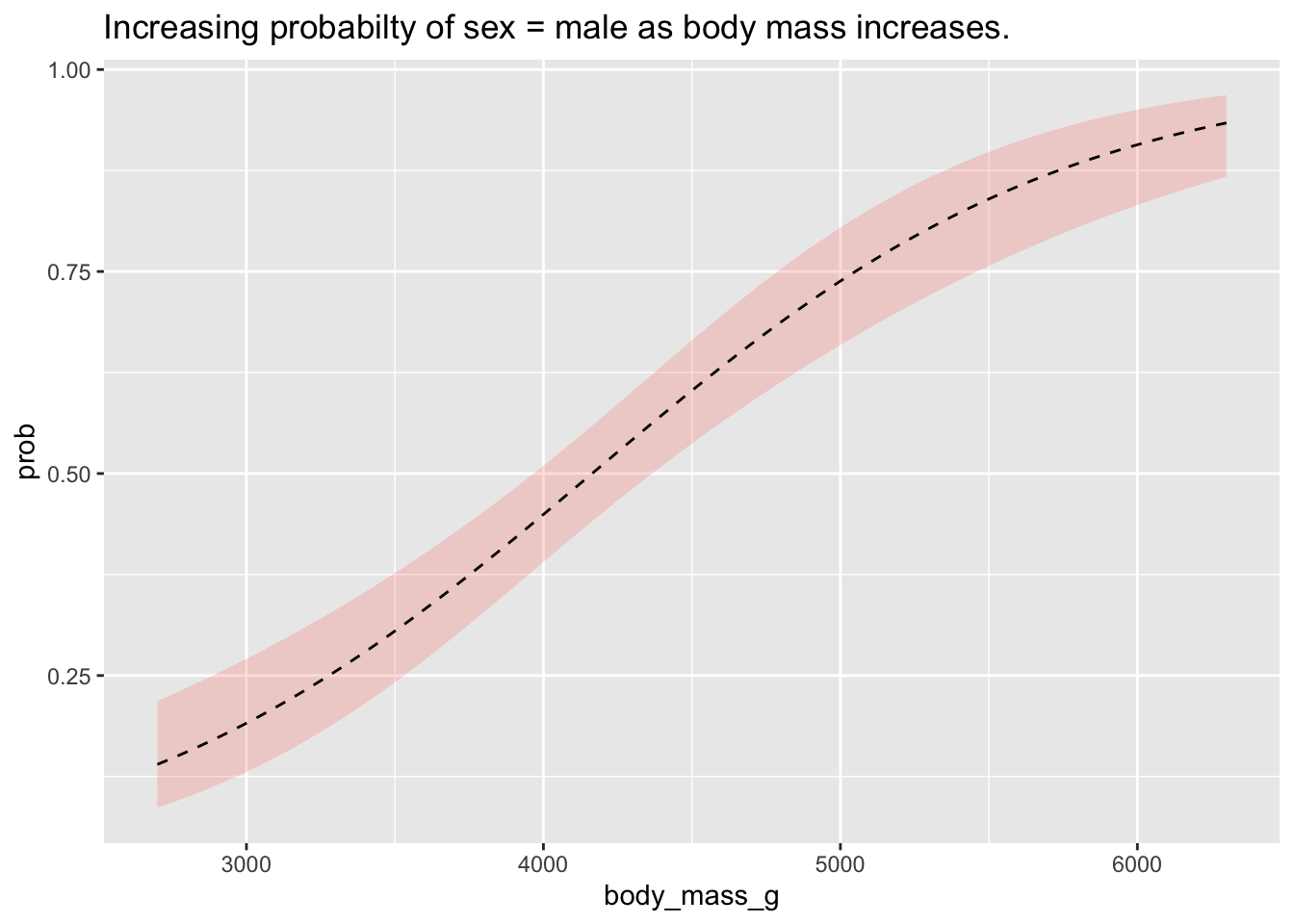
Once you understand how a logistic regression can be interpreted, it becomes no different than the linear regressions we’ve been looking at before. The tricky bit is usually making sure we understand the difference between logits (also called log odds), odds ratios, and probabilities.