emmeans

This notebook expands upon previous lessons by thinking about what the emmeans package is actually doing when we obtain information about a fit model. The goal is to practice interpreting main effects and interactions, and to better understand what a marginal / estimated mean actually…means.

library(tidyverse)
library(palmerpenguins)
library(emmeans)
data(penguins)

penguins <- drop_na(penguins)

Let’s further explore how the package emmeans words to unpack regression model effects. In doing so, we will remind ourselves about how to interpret regression effects and interactions.

# z-score flipper length
penguins$flipper_length_mm_z <- (penguins$flipper_length_mm - mean(penguins$flipper_length_mm)) / 
  sd(penguins$flipper_length_mm)
summary(penguins$flipper_length_mm_z)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
## -2.0667 -0.7825 -0.2830  0.0000  0.8585  2.1428

Let’s fit a model in with a categorical interaction between sex and species, as well as the main effect of flipper length. Do you remember how to interpret this?

m1 <- lm(body_mass_g ~ sex*species + flipper_length_mm_z, data = penguins)
summary(m1)

## 
## Call:
## lm(formula = body_mass_g ~ sex * species + flipper_length_mm_z, 
##     data = penguins)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -832.63 -195.61   -1.39  187.86  826.25 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               3638.69      50.01  72.764  < 2e-16 ***
## sexmale                    580.08      49.30  11.767  < 2e-16 ***
## speciesChinstrap            77.64      60.68   1.280    0.202    
## speciesGentoo              800.55      86.33   9.273  < 2e-16 ***
## flipper_length_mm_z        287.13      39.38   7.291 2.34e-12 ***
## sexmale:speciesChinstrap  -335.82      84.96  -3.953 9.48e-05 ***
## sexmale:speciesGentoo       44.03      71.97   0.612    0.541    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 287.3 on 326 degrees of freedom
## Multiple R-squared:  0.875,  Adjusted R-squared:  0.8727 
## F-statistic: 380.2 on 6 and 326 DF,  p-value: < 2.2e-16

• The intercept reflects the baseline level of all categorical variables and all numerical variables held at 0. So in this model, the baseline of 3638 grams is the predicted body weight of female Adelie penguins.

• sexmale is the difference between the level male in the variable sex and the baseline: female. Because of the interaction, this is the difference between body mass for male and female Adelie penguins. Male Adelie penguins are predicted to weight 580 grams more than female Adelie penguins.

• speciesChinstrap is the difference between the level Chinstrap in the variable species and the baseline: Adelie. Because of the interaction, this is the difference between body mass for female Chinstrap and female Adelie penguins - Female Chinstrap penguins are predicted to weight 77 grams more than Female Adelie penguins.

• speciesGentoo is the difference between the level Gentoo in the variable species and the baseline: Adelie. Because of the interaction, this is the difference between body mass for female Gentoo and female Adelie penguins - Female Gentoo pensuins are predicted to weight 800 grans more than the Female Adelie penguins.

• flipper_length_mm_z is the predicted effect of flipper length on body mass for the baseline (Female Adelia penguins). However, this is a main effect, meaning it will have the same effect across all levels of sex/species (see below.)

The interaction terms

• sexmale:speciesChinstrap is the adjustment to predicted body mass difference between male and female Chinstrap penguins - the coefficient of -355 is subtracted from the sexmale effect to get the predicted difference between male/female Chinstrap penguins.

• sexmale:speciesGentoo is the adjustment to predicted body mass differences between male and female Gentoo penguins - the coefficient of 44 is added to the sexmale effect to get the predicted difference between male/female Gentoo penguins.

What can we not see?

• The difference between male Adelie and male Gentoo penguins
• The difference between male Adelie and male Chinstrap penguins
• The difference between female Gentoo and female Chinstrap penguins
• The difference between the male/female difference for any pairwise comparison

confirming the average effect of flipper length

Make Gentoo the baseline, and fit a new model.

penguins$species <- relevel(penguins$species, ref = 'Gentoo')
summary(penguins$species)

##    Gentoo    Adelie Chinstrap 
##       119       146        68

m2 <- lm(body_mass_g ~ sex*species + flipper_length_mm_z, data = penguins)
summary(m2)

## 
## Call:
## lm(formula = body_mass_g ~ sex * species + flipper_length_mm_z, 
##     data = penguins)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -832.63 -195.61   -1.39  187.86  826.25 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               4439.24      50.11  88.583  < 2e-16 ***
## sexmale                    624.12      58.25  10.715  < 2e-16 ***
## speciesAdelie             -800.55      86.33  -9.273  < 2e-16 ***
## speciesChinstrap          -722.91      85.58  -8.447 9.99e-16 ***
## flipper_length_mm_z        287.13      39.38   7.291 2.34e-12 ***
## sexmale:speciesAdelie      -44.03      71.97  -0.612    0.541    
## sexmale:speciesChinstrap  -379.86      87.39  -4.347 1.85e-05 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 287.3 on 326 degrees of freedom
## Multiple R-squared:  0.875,  Adjusted R-squared:  0.8727 
## F-statistic: 380.2 on 6 and 326 DF,  p-value: < 2.2e-16

Swap it back to Adelie

penguins$species <- relevel(penguins$species, ref = 'Adelie')
summary(penguins$species)

##    Adelie    Gentoo Chinstrap 
##       146       119        68

the emmeans package

The problems with interpreting the regression comparisons become even more complex once we add even more interactions.

The emmeans package lets us obtain marginal and conditional effects of all predictors in our model.

Some terminological points:

• marginal effect: the effect of a \(x\) on \(y\) (i.e., the slope)
  • the slope of a continuous \(x\)
  • the conditional effect of levels of a categorical \(x\)

emmeans will first compute the average values of \(x\), then fit these averaged values using the regression formula, to provide the effect of a predictor when it is at its average - the estimated marginal mean. - emmean: estimate marginal mean: the marginal effect of \(x\) on \(y\) at the mean of \(x\) - emtrend: average slope of continuous \(x\) on \(y\)

basic emmeans usage

The simplest way to use emmeans is to ask for predicted values of \(y\) for a particular variable. The syntax is emmeans(model, ~ effects).

To get the emmean of body_mass_g at different levels of sex, we type:

# what is the estimated marginal effect of sex on body mass?
emmeans(m1, ~ sex)

## NOTE: Results may be misleading due to involvement in interactions

##  sex    emmean   SE  df lower.CL upper.CL
##  female   3931 25.6 326     3881     3982
##  male     4414 25.5 326     4364     4464
## 
## Results are averaged over the levels of: species 
## Confidence level used: 0.95

And the same for species…:

# what is the estimated marginal effect of species on body mass?
emmeans(m1, ~ species)

## NOTE: Results may be misleading due to involvement in interactions

##  species   emmean   SE  df lower.CL upper.CL
##  Adelie      3929 38.7 326     3853     4005
##  Chinstrap   3838 37.7 326     3764     3913
##  Gentoo      4751 52.5 326     4648     4855
## 
## Results are averaged over the levels of: sex 
## Confidence level used: 0.95

And for flipper length:

why do we only get one emmean here?

Because this is the effect of flipper length on body mass when flipper length is at its mean

emmeans(m1, ~ flipper_length_mm_z)

##  flipper_length_mm_z emmean   SE  df lower.CL upper.CL
##              3.5e-16   4173 16.6 326     4140     4205
## 
## Results are averaged over the levels of: sex, species 
## Confidence level used: 0.95

Of course, our model has an interaction, as the warnings have been trying to tell us. We can model these using similar syntax as the lm call. Here we get the predicted body mass for each level of our interaction:

emmeans(m1, ~ sex*species)

##  sex    species   emmean   SE  df lower.CL upper.CL
##  female Adelie      3639 50.0 326     3540     3737
##  male   Adelie      4219 41.3 326     4137     4300
##  female Chinstrap   3716 55.7 326     3607     3826
##  male   Chinstrap   3961 49.4 326     3863     4058
##  female Gentoo      4439 50.1 326     4341     4538
##  male   Gentoo      5063 68.5 326     4929     5198
## 
## Confidence level used: 0.95

plotting the emmeans

simply convert an emmeans call into a data frame, and it becomes easy to plot:

plot1 <- emmeans(m1, ~ sex*species)%>% as.data.frame()

ggplot(plot1, aes(y = emmean, x = species, fill = sex, color = sex)) + 
  geom_point() + 
  geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL), width = .2)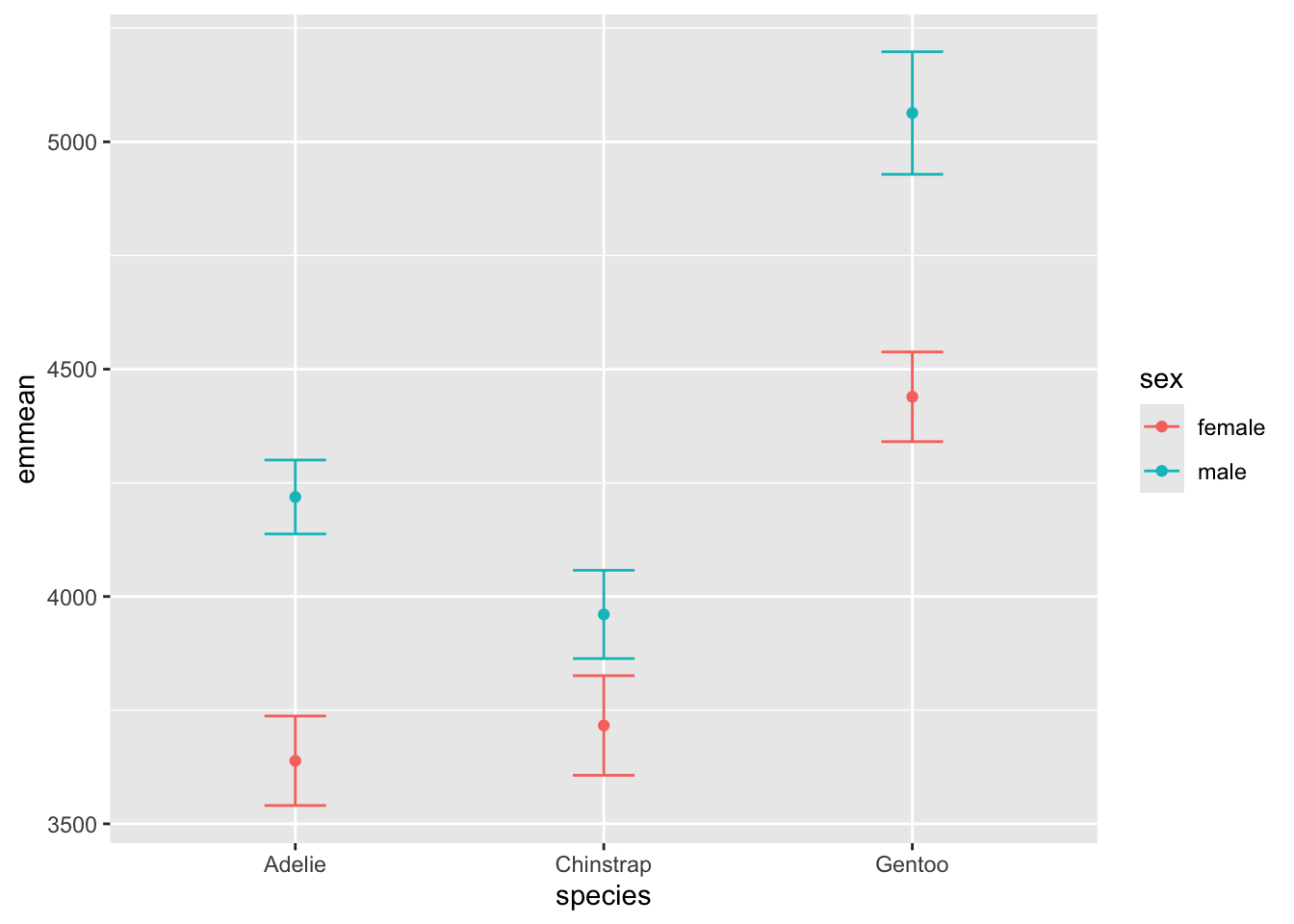

remember those pairwise comparisons?

We can think about comparisons as both within subjects and between subjects.

The within subjects comparison will ask whether the difference in body mass between male/female penguins is “significant” for each species. The between subjects comparison could ask whether male or female penguins differ from other male or female penguins across different species

To do so, we can use the pairwise argument in emmeans to ask for a contrast:

Pairwise contrasts of species…

# test whether body mass differs among species of penguins
emmeans(m1, pairwise ~ species)

## NOTE: Results may be misleading due to involvement in interactions

## $emmeans
##  species   emmean   SE  df lower.CL upper.CL
##  Adelie      3929 38.7 326     3853     4005
##  Chinstrap   3838 37.7 326     3764     3913
##  Gentoo      4751 52.5 326     4648     4855
## 
## Results are averaged over the levels of: sex 
## Confidence level used: 0.95 
## 
## $contrasts
##  contrast           estimate   SE  df t.ratio p.value
##  Adelie - Chinstrap     90.3 45.1 326   2.000  0.1139
##  Adelie - Gentoo      -822.6 83.8 326  -9.815  <.0001
##  Chinstrap - Gentoo   -912.8 74.1 326 -12.320  <.0001
## 
## Results are averaged over the levels of: sex 
## P value adjustment: tukey method for comparing a family of 3 estimates

Pairwise contrasts of sex…

# test whether body mass differs among sex of penguins
emmeans(m1, pairwise ~ sex)

## NOTE: Results may be misleading due to involvement in interactions

## $emmeans
##  sex    emmean   SE  df lower.CL upper.CL
##  female   3931 25.6 326     3881     3982
##  male     4414 25.5 326     4364     4464
## 
## Results are averaged over the levels of: species 
## Confidence level used: 0.95 
## 
## $contrasts
##  contrast      estimate   SE  df t.ratio p.value
##  female - male     -483 38.9 326 -12.426  <.0001
## 
## Results are averaged over the levels of: species

ALL the pairwise!!

Ask yourself - how many of these comparisons do we actually want?

emmeans(m1, pairwise ~ sex*species)

## $emmeans
##  sex    species   emmean   SE  df lower.CL upper.CL
##  female Adelie      3639 50.0 326     3540     3737
##  male   Adelie      4219 41.3 326     4137     4300
##  female Chinstrap   3716 55.7 326     3607     3826
##  male   Chinstrap   3961 49.4 326     3863     4058
##  female Gentoo      4439 50.1 326     4341     4538
##  male   Gentoo      5063 68.5 326     4929     5198
## 
## Confidence level used: 0.95 
## 
## $contrasts
##  contrast                          estimate    SE  df t.ratio p.value
##  female Adelie - male Adelie         -580.1  49.3 326 -11.767  <.0001
##  female Adelie - female Chinstrap     -77.6  60.7 326  -1.280  0.7961
##  female Adelie - male Chinstrap      -321.9  68.7 326  -4.686  0.0001
##  female Adelie - female Gentoo       -800.5  86.3 326  -9.273  <.0001
##  female Adelie - male Gentoo        -1424.7 107.1 326 -13.300  <.0001
##  male Adelie - female Chinstrap       502.4  59.7 326   8.418  <.0001
##  male Adelie - male Chinstrap         258.2  63.3 326   4.081  0.0008
##  male Adelie - female Gentoo         -220.5  76.2 326  -2.893  0.0464
##  male Adelie - male Gentoo           -844.6  95.8 326  -8.814  <.0001
##  female Chinstrap - male Chinstrap   -244.3  73.4 326  -3.329  0.0124
##  female Chinstrap - female Gentoo    -722.9  85.6 326  -8.447  <.0001
##  female Chinstrap - male Gentoo     -1347.0 103.9 326 -12.965  <.0001
##  male Chinstrap - female Gentoo      -478.6  71.7 326  -6.674  <.0001
##  male Chinstrap - male Gentoo       -1102.8  86.5 326 -12.755  <.0001
##  female Gentoo - male Gentoo         -624.1  58.2 326 -10.715  <.0001
## 
## P value adjustment: tukey method for comparing a family of 6 estimates

A more sensible approach is to ask for conditional effects using the pipe: |

Compare the between group effect of species at among females and among males (no male-female cross-species comparisons)

emmeans(m1, pairwise ~ species|sex)$contrasts

## sex = female:
##  contrast           estimate   SE  df t.ratio p.value
##  Adelie - Chinstrap    -77.6 60.7 326  -1.280  0.4077
##  Adelie - Gentoo      -800.5 86.3 326  -9.273  <.0001
##  Chinstrap - Gentoo   -722.9 85.6 326  -8.447  <.0001
## 
## sex = male:
##  contrast           estimate   SE  df t.ratio p.value
##  Adelie - Chinstrap    258.2 63.3 326   4.081  0.0002
##  Adelie - Gentoo      -844.6 95.8 326  -8.814  <.0001
##  Chinstrap - Gentoo  -1102.8 86.5 326 -12.755  <.0001
## 
## P value adjustment: tukey method for comparing a family of 3 estimates

Compare the within group effect of sex in each species. Is it really very interesting to us that all males > females?

And, which of these effects do we see in the model output?

emmeans(m1, pairwise ~ sex|species)$contrasts

## species = Adelie:
##  contrast      estimate   SE  df t.ratio p.value
##  female - male     -580 49.3 326 -11.767  <.0001
## 
## species = Chinstrap:
##  contrast      estimate   SE  df t.ratio p.value
##  female - male     -244 73.4 326  -3.329  0.0010
## 
## species = Gentoo:
##  contrast      estimate   SE  df t.ratio p.value
##  female - male     -624 58.2 326 -10.715  <.0001

# here is the output as reminder
summary(m1)

## 
## Call:
## lm(formula = body_mass_g ~ sex * species + flipper_length_mm_z, 
##     data = penguins)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -832.63 -195.61   -1.39  187.86  826.25 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               3638.69      50.01  72.764  < 2e-16 ***
## sexmale                    580.08      49.30  11.767  < 2e-16 ***
## speciesChinstrap            77.64      60.68   1.280    0.202    
## speciesGentoo              800.55      86.33   9.273  < 2e-16 ***
## flipper_length_mm_z        287.13      39.38   7.291 2.34e-12 ***
## sexmale:speciesChinstrap  -335.82      84.96  -3.953 9.48e-05 ***
## sexmale:speciesGentoo       44.03      71.97   0.612    0.541    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 287.3 on 326 degrees of freedom
## Multiple R-squared:  0.875,  Adjusted R-squared:  0.8727 
## F-statistic: 380.2 on 6 and 326 DF,  p-value: < 2.2e-16

and compare the size of the interaction

emmeans(m1, pairwise ~ sex*species, interaction = 'pairwise')$contrasts

##  sex_pairwise  species_pairwise   estimate   SE  df t.ratio p.value
##  female - male Adelie - Chinstrap     -336 85.0 326  -3.953  0.0001
##  female - male Adelie - Gentoo          44 72.0 326   0.612  0.5410
##  female - male Chinstrap - Gentoo      380 87.4 326   4.347  <.0001

Again, which of these can we see in the summary output?

summary(m1)

## 
## Call:
## lm(formula = body_mass_g ~ sex * species + flipper_length_mm_z, 
##     data = penguins)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -832.63 -195.61   -1.39  187.86  826.25 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               3638.69      50.01  72.764  < 2e-16 ***
## sexmale                    580.08      49.30  11.767  < 2e-16 ***
## speciesChinstrap            77.64      60.68   1.280    0.202    
## speciesGentoo              800.55      86.33   9.273  < 2e-16 ***
## flipper_length_mm_z        287.13      39.38   7.291 2.34e-12 ***
## sexmale:speciesChinstrap  -335.82      84.96  -3.953 9.48e-05 ***
## sexmale:speciesGentoo       44.03      71.97   0.612    0.541    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 287.3 on 326 degrees of freedom
## Multiple R-squared:  0.875,  Adjusted R-squared:  0.8727 
## F-statistic: 380.2 on 6 and 326 DF,  p-value: < 2.2e-16

finally….what about flipper length?

We have the predicted body mass of penguins when flipper length is held at its mean:

emmeans(m1, ~ flipper_length_mm_z)

##  flipper_length_mm_z emmean   SE  df lower.CL upper.CL
##              3.5e-16   4173 16.6 326     4140     4205
## 
## Results are averaged over the levels of: sex, species 
## Confidence level used: 0.95

To obtain the average effect of flipper length, or more specifically, the effect of flipper length when it is held at its mean, we use emtrends() for continuous trends (slopes)

emtrends(m1, ~ flipper_length_mm_z, var = 'flipper_length_mm_z')

##  flipper_length_mm_z flipper_length_mm_z.trend   SE  df lower.CL upper.CL
##              3.5e-16                       287 39.4 326      210      365
## 
## Results are averaged over the levels of: sex, species 
## Confidence level used: 0.95

This is, of course, exactly what the regression model output will show us:

summary(m1)

## 
## Call:
## lm(formula = body_mass_g ~ sex * species + flipper_length_mm_z, 
##     data = penguins)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -832.63 -195.61   -1.39  187.86  826.25 
## 
## Coefficients:
##                          Estimate Std. Error t value Pr(>|t|)    
## (Intercept)               3638.69      50.01  72.764  < 2e-16 ***
## sexmale                    580.08      49.30  11.767  < 2e-16 ***
## speciesChinstrap            77.64      60.68   1.280    0.202    
## speciesGentoo              800.55      86.33   9.273  < 2e-16 ***
## flipper_length_mm_z        287.13      39.38   7.291 2.34e-12 ***
## sexmale:speciesChinstrap  -335.82      84.96  -3.953 9.48e-05 ***
## sexmale:speciesGentoo       44.03      71.97   0.612    0.541    
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 287.3 on 326 degrees of freedom
## Multiple R-squared:  0.875,  Adjusted R-squared:  0.8727 
## F-statistic: 380.2 on 6 and 326 DF,  p-value: < 2.2e-16

We can plug in a range of different values for flipper_length_mm_z to emtrend() to see how it moves across values in our data.

flipper_range = seq(from = min(penguins$flipper_length_mm_z), to = max(penguins$flipper_length_mm_z), by = .1)
emtrends(m1, ~ flipper_length_mm_z, var = 'flipper_length_mm_z', at = list(flipper_length_mm_z = flipper_range))

##  flipper_length_mm_z flipper_length_mm_z.trend   SE  df lower.CL upper.CL
##              -2.0667                       287 39.4 326      210      365
##              -1.9667                       287 39.4 326      210      365
##              -1.8667                       287 39.4 326      210      365
##              -1.7667                       287 39.4 326      210      365
##              -1.6667                       287 39.4 326      210      365
##              -1.5667                       287 39.4 326      210      365
##              -1.4667                       287 39.4 326      210      365
##              -1.3667                       287 39.4 326      210      365
##              -1.2667                       287 39.4 326      210      365
##              -1.1667                       287 39.4 326      210      365
##              -1.0667                       287 39.4 326      210      365
##              -0.9667                       287 39.4 326      210      365
##              -0.8667                       287 39.4 326      210      365
##              -0.7667                       287 39.4 326      210      365
##              -0.6667                       287 39.4 326      210      365
##              -0.5667                       287 39.4 326      210      365
##              -0.4667                       287 39.4 326      210      365
##              -0.3667                       287 39.4 326      210      365
##              -0.2667                       287 39.4 326      210      365
##              -0.1667                       287 39.4 326      210      365
##              -0.0667                       287 39.4 326      210      365
##               0.0333                       287 39.4 326      210      365
##               0.1333                       287 39.4 326      210      365
##               0.2333                       287 39.4 326      210      365
##               0.3333                       287 39.4 326      210      365
##               0.4333                       287 39.4 326      210      365
##               0.5333                       287 39.4 326      210      365
##               0.6333                       287 39.4 326      210      365
##               0.7333                       287 39.4 326      210      365
##               0.8333                       287 39.4 326      210      365
##               0.9333                       287 39.4 326      210      365
##               1.0333                       287 39.4 326      210      365
##               1.1333                       287 39.4 326      210      365
##               1.2333                       287 39.4 326      210      365
##               1.3333                       287 39.4 326      210      365
##               1.4333                       287 39.4 326      210      365
##               1.5333                       287 39.4 326      210      365
##               1.6333                       287 39.4 326      210      365
##               1.7333                       287 39.4 326      210      365
##               1.8333                       287 39.4 326      210      365
##               1.9333                       287 39.4 326      210      365
##               2.0333                       287 39.4 326      210      365
##               2.1333                       287 39.4 326      210      365
## 
## Results are averaged over the levels of: sex, species 
## Confidence level used: 0.95

That gives us a lot of values…better to plot it? We can use the emmip function to make a plot grid.

# pretty!
flipper_plot <- as.data.frame(emmip(m1, ~ flipper_length_mm_z, var = 'flipper_length_mm_z', at = list(flipper_length_mm_z = flipper_range), CIs = TRUE, plotit = F))


ggplot(flipper_plot, aes(x = flipper_length_mm_z, y = yvar)) + 
  geom_ribbon(aes(ymin = LCL, ymax = UCL), alpha = .2) + 
  geom_line() + 
  labs(y = 'Body Mass (g)', x = 'Flipper Length (z-scored)')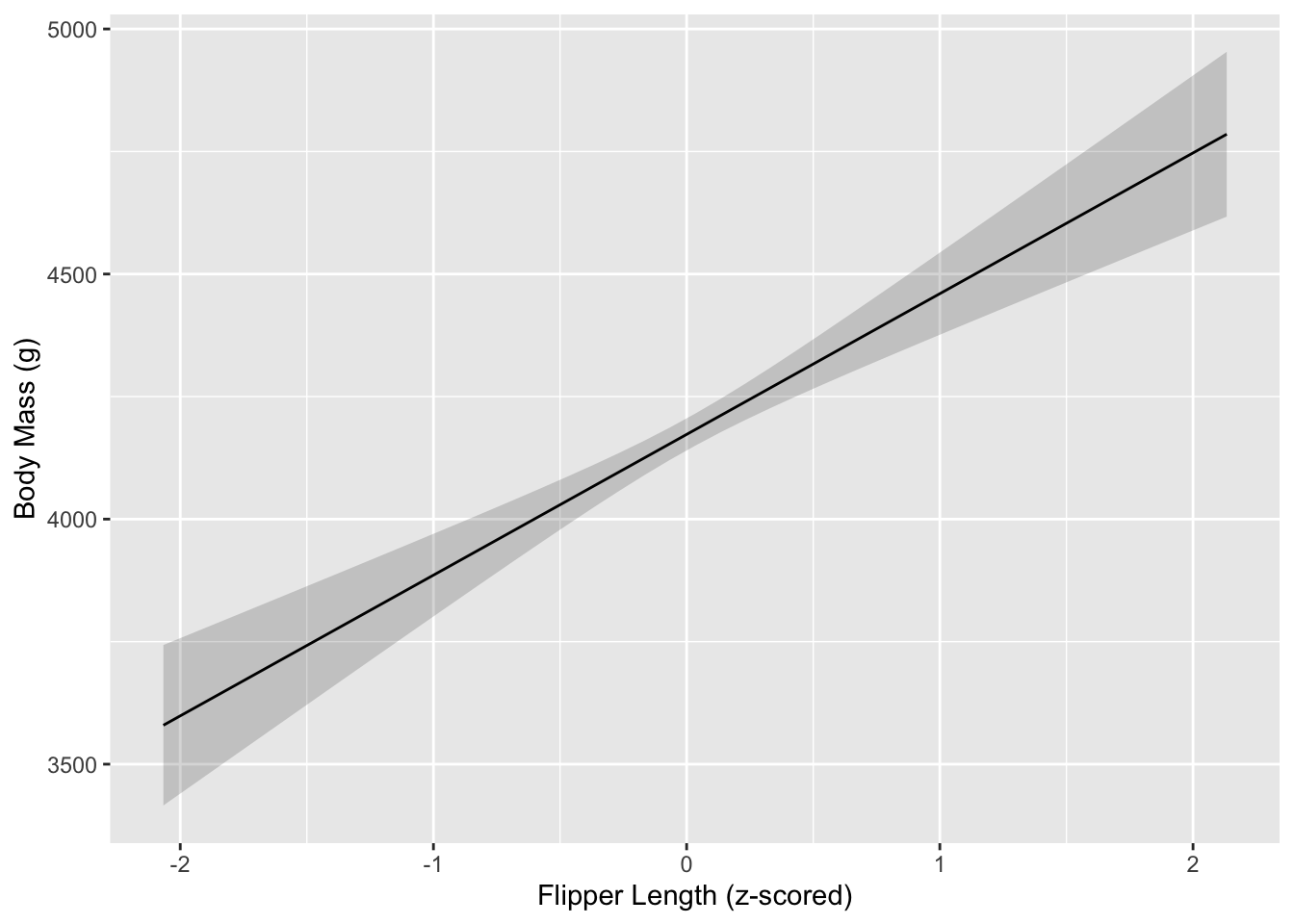

But we can also use emmeans to get predicted body mass at different levels of flipper length…

emmeans(m1, ~ flipper_length_mm_z, at = list(flipper_length_mm_z = flipper_range))

##  flipper_length_mm_z emmean   SE  df lower.CL upper.CL
##              -2.0667   3579 83.2 326     3416     3743
##              -1.9667   3608 79.3 326     3452     3764
##              -1.8667   3637 75.5 326     3488     3785
##              -1.7667   3666 71.7 326     3525     3807
##              -1.6667   3694 67.8 326     3561     3828
##              -1.5667   3723 64.0 326     3597     3849
##              -1.4667   3752 60.2 326     3633     3870
##              -1.3667   3780 56.5 326     3669     3891
##              -1.2667   3809 52.7 326     3705     3913
##              -1.1667   3838 49.0 326     3741     3934
##              -1.0667   3867 45.3 326     3777     3956
##              -0.9667   3895 41.7 326     3813     3977
##              -0.8667   3924 38.1 326     3849     3999
##              -0.7667   3953 34.6 326     3885     4021
##              -0.6667   3981 31.2 326     3920     4043
##              -0.5667   4010 27.9 326     3955     4065
##              -0.4667   4039 24.9 326     3990     4088
##              -0.3667   4068 22.1 326     4024     4111
##              -0.2667   4096 19.7 326     4057     4135
##              -0.1667   4125 17.9 326     4090     4160
##              -0.0667   4154 16.8 326     4121     4187
##               0.0333   4182 16.6 326     4150     4215
##               0.1333   4211 17.3 326     4177     4245
##               0.2333   4240 18.9 326     4203     4277
##               0.3333   4269 21.1 326     4227     4310
##               0.4333   4297 23.7 326     4251     4344
##               0.5333   4326 26.6 326     4274     4378
##               0.6333   4355 29.8 326     4296     4413
##               0.7333   4383 33.2 326     4318     4449
##               0.8333   4412 36.6 326     4340     4484
##               0.9333   4441 40.2 326     4362     4520
##               1.0333   4470 43.8 326     4383     4556
##               1.1333   4498 47.5 326     4405     4592
##               1.2333   4527 51.2 326     4426     4628
##               1.3333   4556 54.9 326     4448     4664
##               1.4333   4584 58.7 326     4469     4700
##               1.5333   4613 62.5 326     4490     4736
##               1.6333   4642 66.3 326     4511     4772
##               1.7333   4670 70.1 326     4533     4808
##               1.8333   4699 73.9 326     4554     4845
##               1.9333   4728 77.8 326     4575     4881
##               2.0333   4757 81.6 326     4596     4917
##               2.1333   4785 85.5 326     4617     4954
## 
## Results are averaged over the levels of: sex, species 
## Confidence level used: 0.95

Plotting this shows us that…

# it's the exact same plot!!!!

p3 <- as.data.frame(emmeans(m1, ~ flipper_length_mm_z, at = list(flipper_length_mm_z = flipper_range)))

ggplot(p3, aes(y = emmean, x = flipper_length_mm_z)) + 
  geom_ribbon(aes(ymin = lower.CL, ymax = upper.CL), alpha = .2) + 
  geom_line()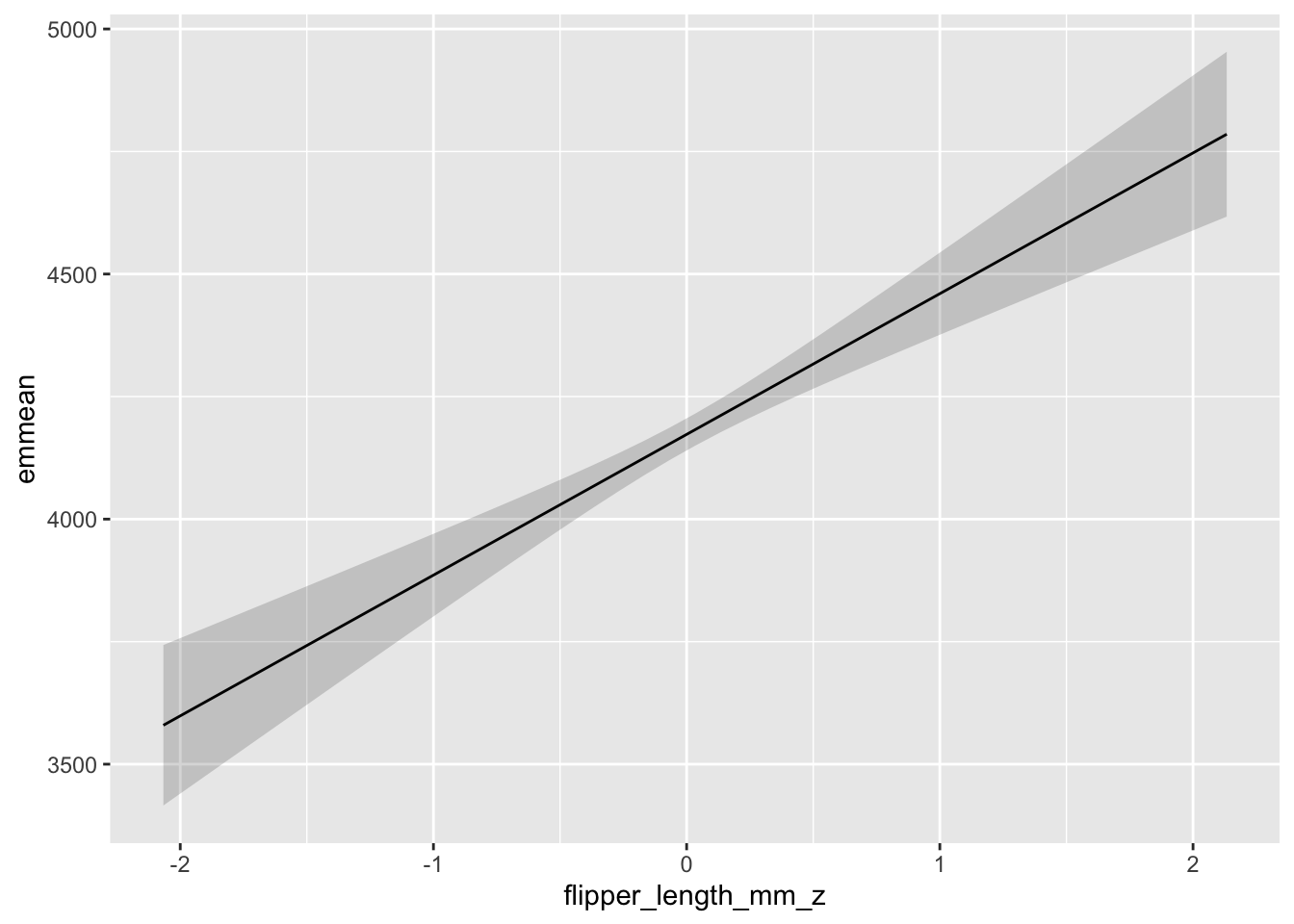

Actually, the average effect from emmeans is just one way of doing these things - it provides the answer to the “average case” in our data. This is slightly different than the actual average effect in our population…but that requires a different approach. Maybe for next time!