categorical by categorical
Stephen Skalicky
2024-12-04
In this notebook we will consider a third type of interaction - categorical by categorical. We will further complicate this by using a two level * three level categorical interaction.
We will ask the question is there an interaction between penguin species and sex on body mass?
Before moving on, please consider what this interaction is asking. Recall that an interaction is a conditional effect, meaning that the effect of one variable depends on another.
# load libraries
library(tidyverse)
library(palmerpenguins)
library(emmeans)
data(penguins)
penguins <- drop_na(penguins)We already know that sex has a significant “effect” on body weight, as we’ve already explored it before. The default dummy coding scheme. Here we see that, on average, penguin males are 683 grams heavier than penguin females.
##
## Call:
## lm(formula = body_mass_g ~ sex, data = penguins)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1295.7 -595.7 -237.3 737.7 1754.3
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3862.27 56.83 67.963 < 2e-16 ***
## sexmale 683.41 80.01 8.542 4.9e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 730 on 331 degrees of freedom
## Multiple R-squared: 0.1806, Adjusted R-squared: 0.1781
## F-statistic: 72.96 on 1 and 331 DF, p-value: 4.897e-16Look at the effects of species
Then what does an interaction ask for? It will ask whether this male-female difference depends on or is conditional on penguin species.
Now let’s look at species, which is a three-level categorical variable
## [1] "Adelie" "Chinstrap" "Gentoo"We can see the number of cases per level:
## Adelie Chinstrap Gentoo
## 146 68 119We have some evidence that body mass is different among penguin species.
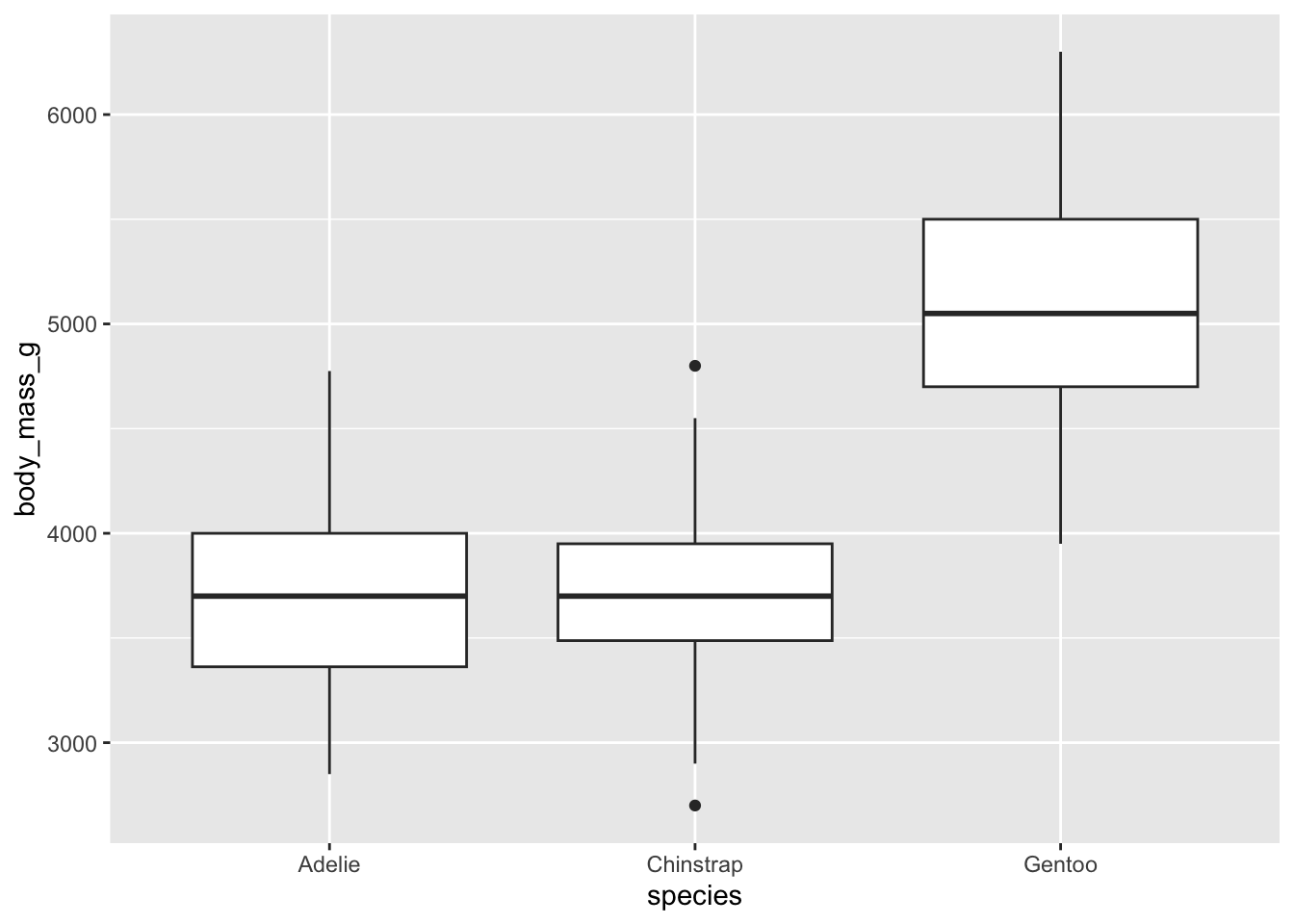
And we can see the way the contrast coding works for dummy variables. What does it mean for both Chinstrap and Gentoo to be coded as 1, with Adelie as 0?
## Chinstrap Gentoo
## Adelie 0 0
## Chinstrap 1 0
## Gentoo 0 1Fitting a model may help to demonstrate the effect - note that we have two coefficients, one for Chinstrap, and one for Gentoo. They are both being compared to the baseline level - Adelie. So when compared to Adelia, Chinstrap has a body mass on average 27 grams heavier, and Gentoo have a body mass on average 1386 grams heavier.
##
## Call:
## lm(formula = body_mass_g ~ species, data = penguins)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1142.44 -342.44 -33.09 307.56 1207.56
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3706.16 38.14 97.184 <2e-16 ***
## speciesChinstrap 26.92 67.65 0.398 0.691
## speciesGentoo 1386.27 56.91 24.359 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 460.8 on 330 degrees of freedom
## Multiple R-squared: 0.6745, Adjusted R-squared: 0.6725
## F-statistic: 341.9 on 2 and 330 DF, p-value: < 2.2e-16What contrast are we missing…? Fortunately we can use another library to get these contrasts, but more on that later. But, look, we can see that the contrast between Adelie and Chinstrap is not significant, whereas the other contrasts are!
## $emmeans
## species emmean SE df lower.CL upper.CL
## Adelie 3706 38.1 330 3631 3781
## Chinstrap 3733 55.9 330 3623 3843
## Gentoo 5092 42.2 330 5009 5176
##
## Confidence level used: 0.95
##
## $contrasts
## contrast estimate SE df t.ratio p.value
## Adelie - Chinstrap -26.9 67.7 330 -0.398 0.9164
## Adelie - Gentoo -1386.3 56.9 330 -24.359 <.0001
## Chinstrap - Gentoo -1359.3 70.0 330 -19.406 <.0001
##
## P value adjustment: tukey method for comparing a family of 3 estimatesLet’s look at this with contrast coding, where we now have 3 levels of our variable turned into sum coding. Each column will sum to 0.
Previously, with 2 levels, 0 represented the “midpoint” between the two groups if they were coded as -1 and 1.
Here it is different. The group with a 1 is now compared to the other two groups - note that 0 + -1 = -1. So 0 becomes the “midpoint” between the group coded as 1 and the average of the other two groups.
## [,1] [,2]
## Adelie 1 0
## Chinstrap 0 1
## Gentoo -1 -1With that in mind, can we interpret this regression?
The coefficients go in the same order as the levels of the variable
Species 1 = Adelie Species 2 = Chinstrap
The intercept is the grant mean of all penguins
So species1 is the deviation of Adelie compared to the
mean of Chinstrap + Gentoo
And species2 is the deviation of Chinstrap from the mean
of Adelie + Gentoo
What do we lose/gain with this approach?
##
## Call:
## lm(formula = body_mass_g ~ species, data = penguins)
##
## Residuals:
## Min 1Q Median 3Q Max
## -1142.44 -342.44 -33.09 307.56 1207.56
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 4177.23 26.59 157.12 <2e-16 ***
## species1 -471.07 34.52 -13.65 <2e-16 ***
## species2 -444.14 41.80 -10.62 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 460.8 on 330 degrees of freedom
## Multiple R-squared: 0.6745, Adjusted R-squared: 0.6725
## F-statistic: 341.9 on 2 and 330 DF, p-value: < 2.2e-16Regardless of coding, when we plot the model predictions, we know we are just getting the mean body mass at these different species:
## species emmean SE df lower.CL upper.CL
## Adelie 3706.164 38.13563 330 3631.145 3781.184
## Chinstrap 3733.088 55.87955 330 3623.163 3843.013
## Gentoo 5092.437 42.24097 330 5009.341 5175.533
##
## Confidence level used: 0.95ggplot(m3_emmeans, aes(y = emmean, x = species)) +
geom_point() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL),width = .2) +
labs(title = 'literally just their mean body mass')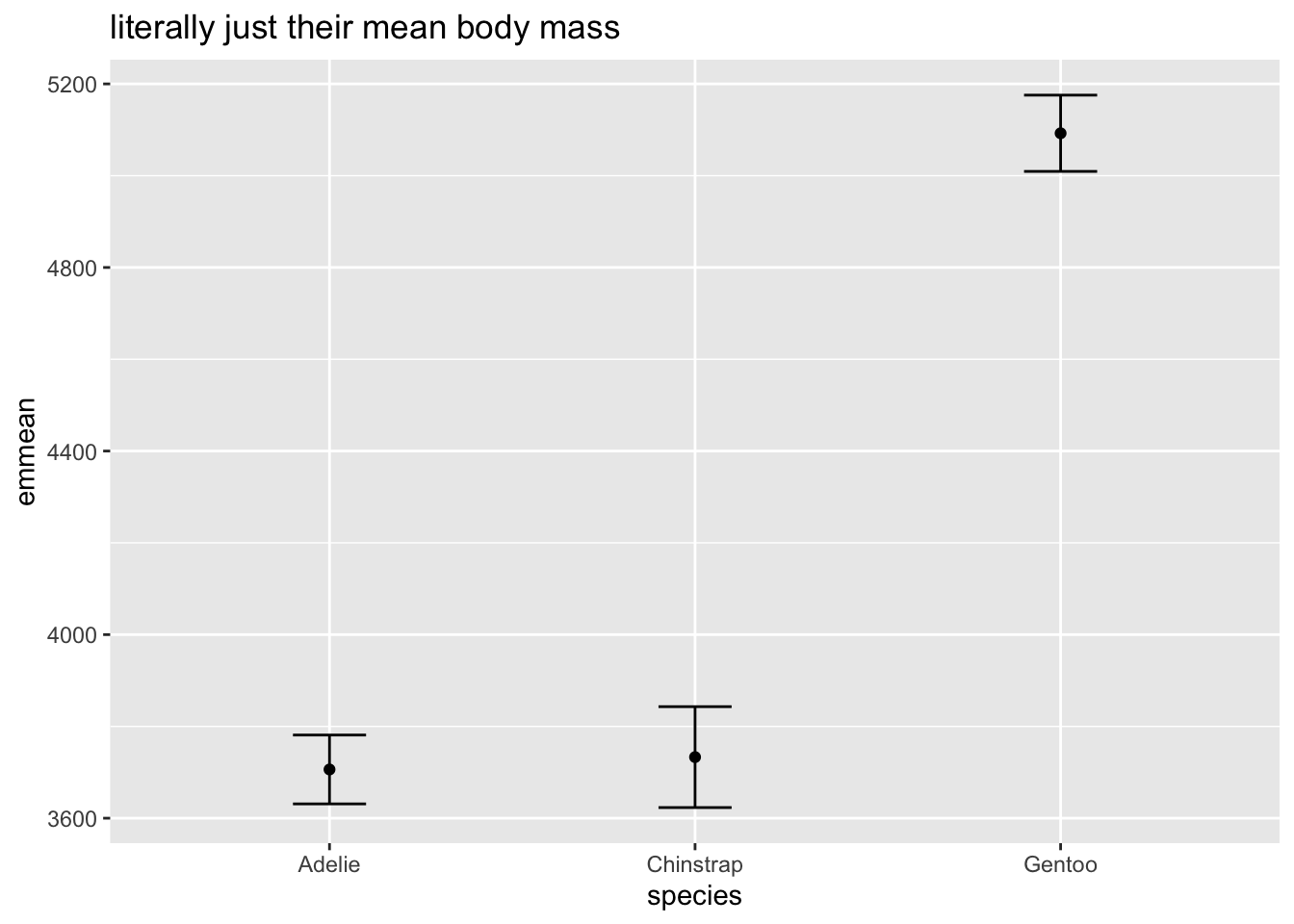
actually fit the interactions
reset species to dummy coding
## Chinstrap Gentoo
## Adelie 0 0
## Chinstrap 1 0
## Gentoo 0 1Now we are getting more complicated.
The interaction here has made things difficult to interpret
The intercept is when species AND sex is at baseline. So the intercept is Adelie, female penguins.
Everything else is being compared to this intercept -
speciesChinstrap is now comparing the difference between
the variable species and the baseline (intercept). This
means it will be female Chinstrap vs. female Adelie. Same thing for
speciesGentoo.
The coefficient sexmale will then be male Adelie
vs. female Adelie (a difference of 674 grams)
The interaction terms then show us how much to adjust the
sexmale effect for the other two levels of species:
The difference between male and female chinstrap is -262 grams less than the difference between male and female Adelie penguins
The difference between male and female Gentoo is 130 grams more than the difference between male and female Adelie penguins
##
## Call:
## lm(formula = body_mass_g ~ species * sex, data = penguins)
##
## Residuals:
## Min 1Q Median 3Q Max
## -827.21 -213.97 11.03 206.51 861.03
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3368.84 36.21 93.030 < 2e-16 ***
## speciesChinstrap 158.37 64.24 2.465 0.01420 *
## speciesGentoo 1310.91 54.42 24.088 < 2e-16 ***
## sexmale 674.66 51.21 13.174 < 2e-16 ***
## speciesChinstrap:sexmale -262.89 90.85 -2.894 0.00406 **
## speciesGentoo:sexmale 130.44 76.44 1.706 0.08886 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 309.4 on 327 degrees of freedom
## Multiple R-squared: 0.8546, Adjusted R-squared: 0.8524
## F-statistic: 384.3 on 5 and 327 DF, p-value: < 2.2e-16is my interaction ‘significant?’
There are a variety of ways to test if an interaction is significant, one is the model comparison approach
## Analysis of Variance Table
##
## Model 1: body_mass_g ~ species * sex
## Model 2: body_mass_g ~ species + sex
## Res.Df RSS Df Sum of Sq F Pr(>F)
## 1 327 31302628
## 2 329 32979185 -2 -1676557 8.757 0.0001973 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1using emmeans
An invaluable way to decompose a fit model
Emmeans lets us look at estimated marginal means in the model:
## NOTE: Results may be misleading due to involvement in interactions## species emmean SE df lower.CL upper.CL
## Adelie 3706 25.6 327 3656 3757
## Chinstrap 3733 37.5 327 3659 3807
## Gentoo 5082 28.4 327 5026 5138
##
## Results are averaged over the levels of: sex
## Confidence level used: 0.95## NOTE: Results may be misleading due to involvement in interactions## sex emmean SE df lower.CL upper.CL
## female 3859 25.3 327 3809 3908
## male 4489 25.2 327 4440 4539
##
## Results are averaged over the levels of: species
## Confidence level used: 0.95## species sex emmean SE df lower.CL upper.CL
## Adelie female 3369 36.2 327 3298 3440
## Chinstrap female 3527 53.1 327 3423 3632
## Gentoo female 4680 40.6 327 4600 4760
## Adelie male 4043 36.2 327 3972 4115
## Chinstrap male 3939 53.1 327 3835 4043
## Gentoo male 5485 39.6 327 5407 5563
##
## Confidence level used: 0.95The pairwise or pairs functions lets us
make comparisons:
Does this show us the interaction?
## sex = female:
## contrast estimate SE df t.ratio p.value
## Adelie - Chinstrap -158 64.2 327 -2.465 0.0377
## Adelie - Gentoo -1311 54.4 327 -24.088 <.0001
## Chinstrap - Gentoo -1153 66.8 327 -17.246 <.0001
##
## sex = male:
## contrast estimate SE df t.ratio p.value
## Adelie - Chinstrap 105 64.2 327 1.627 0.2357
## Adelie - Gentoo -1441 53.7 327 -26.855 <.0001
## Chinstrap - Gentoo -1546 66.2 327 -23.345 <.0001
##
## P value adjustment: tukey method for comparing a family of 3 estimatesDoes this show us the interaction?
## species = Adelie:
## contrast estimate SE df t.ratio p.value
## female - male -675 51.2 327 -13.174 <.0001
##
## species = Chinstrap:
## contrast estimate SE df t.ratio p.value
## female - male -412 75.0 327 -5.487 <.0001
##
## species = Gentoo:
## contrast estimate SE df t.ratio p.value
## female - male -805 56.7 327 -14.188 <.0001Do either of those posthocs show us the answer to the interaction: does the effect of sex depend on species?
we still don’t know what is “Significant” about this effect!
Let’s look at two different plots
dat <- as.data.frame(emmeans(m4, ~ species|sex))
ggplot(dat, aes(y = emmean, x = sex, color = species, group = species)) +
geom_point() +
geom_line() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL), width = .2) +
labs(title = 'What is the interaction here?')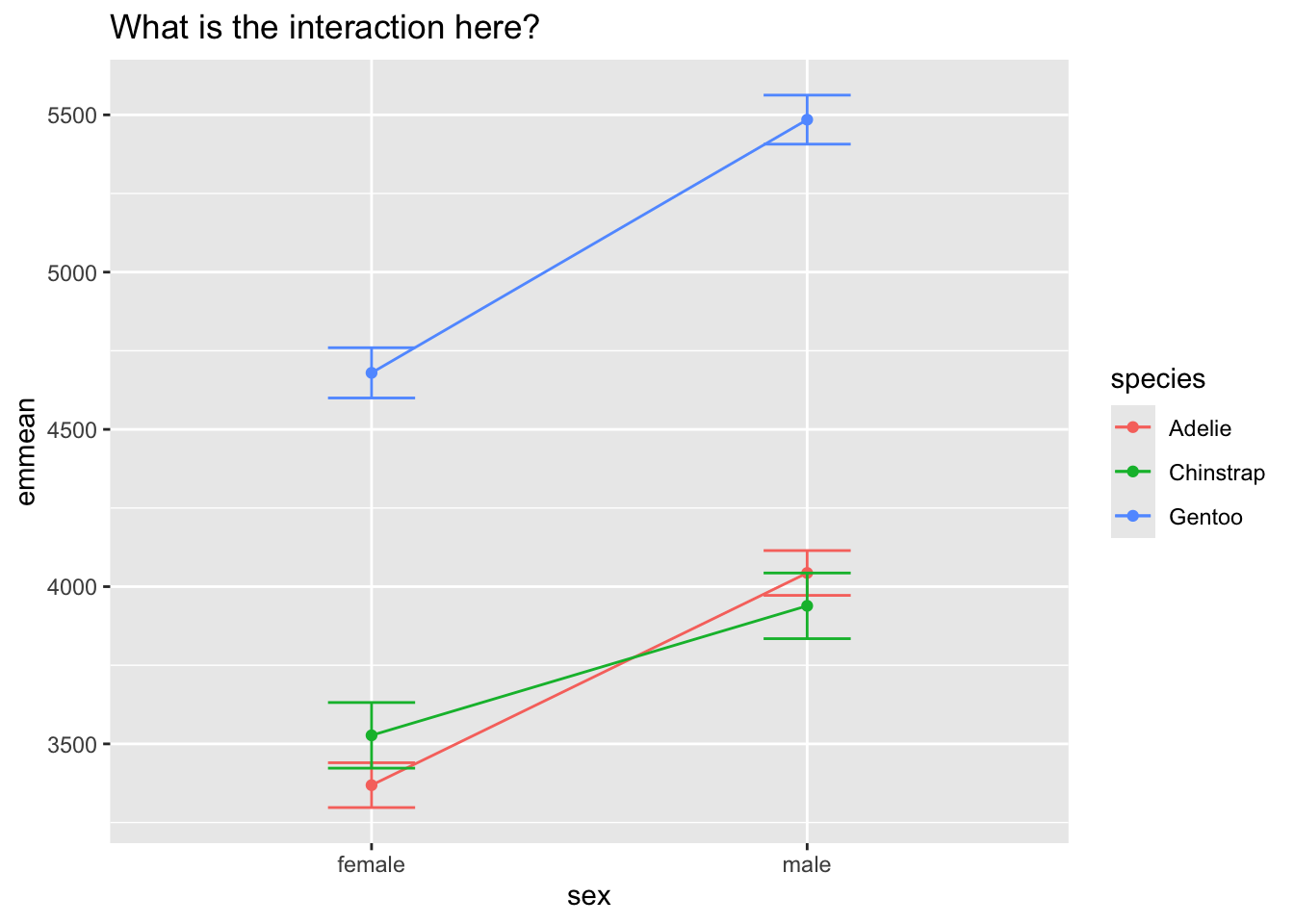
dat <- as.data.frame(emmeans(m4, ~ species|sex))
ggplot(dat, aes(y = emmean, x = species, color = sex, group = sex)) +
geom_point() +
geom_errorbar(aes(ymin = lower.CL, ymax = upper.CL), width = .2) +
labs(title = 'What is the interaction here?')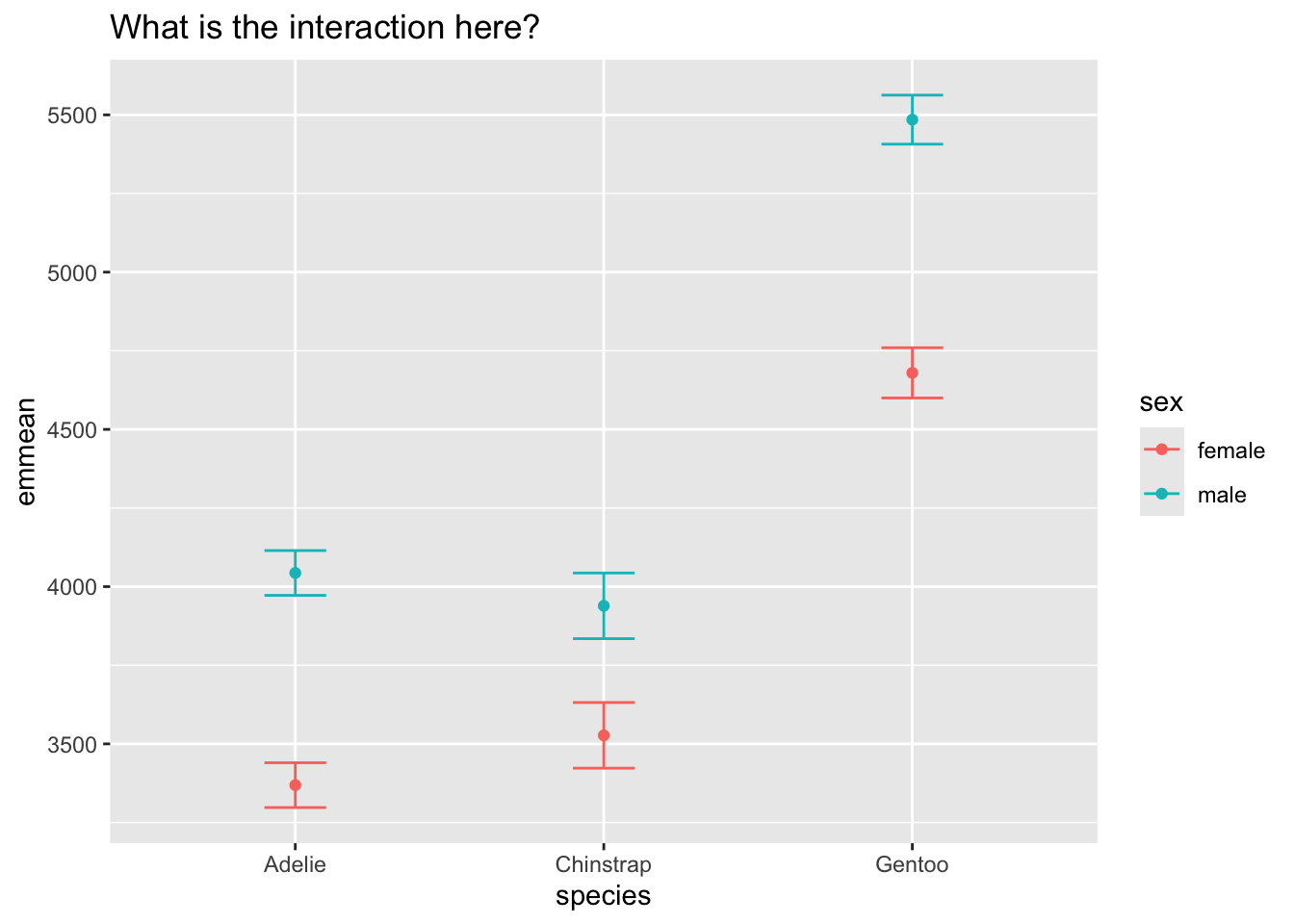
The true reason for the interaction is that the difference between male and female pensguins is stronger for one species when compared to the others. Again, emmeans can show this to us.
Here I ask for the model to show me the differences of differences - and compare them - to find which male/female difference is different/not different among the groups:
Here we see that the difference between female/male is smaller for Chinstrap when compared to Adelie, and larger for Gentoo when compared to Chinstrap
## species_pairwise sex_pairwise estimate SE df t.ratio p.value
## Adelie - Chinstrap female - male -263 90.8 327 -2.894 0.0041
## Adelie - Gentoo female - male 130 76.4 327 1.706 0.0889
## Chinstrap - Gentoo female - male 393 94.1 327 4.181 <.0001Note that the summary almost gave us this whole picture:
##
## Call:
## lm(formula = body_mass_g ~ species * sex, data = penguins)
##
## Residuals:
## Min 1Q Median 3Q Max
## -827.21 -213.97 11.03 206.51 861.03
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 3368.84 36.21 93.030 < 2e-16 ***
## speciesChinstrap 158.37 64.24 2.465 0.01420 *
## speciesGentoo 1310.91 54.42 24.088 < 2e-16 ***
## sexmale 674.66 51.21 13.174 < 2e-16 ***
## speciesChinstrap:sexmale -262.89 90.85 -2.894 0.00406 **
## speciesGentoo:sexmale 130.44 76.44 1.706 0.08886 .
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 309.4 on 327 degrees of freedom
## Multiple R-squared: 0.8546, Adjusted R-squared: 0.8524
## F-statistic: 384.3 on 5 and 327 DF, p-value: < 2.2e-16This shows us again that trying to interpret the effects without post-hoc modeling may indeed drive us to madness.